In the last section, if statements were used to describe simple combinational logic circuits. Synthesizing the Verilog code produced multiplexing circuits, although the exact implementation depends upon the synthesis tool used and the target architecture of the device.
As well as enabling the creation of multiplexers, if statements can also be used to implement tristate buffers and transparent latches. In this article we will look at how transparent latches are synthesized from if statements and how to avoid the inadvertent creation of latches when you meant to create combinational logic circuits from Verilog code containing if statements.
If Statements
In the processes that have been coded up so far, if-else statements rather than simple if statements have been used. Let's use a simple if statement rather than an if-else statement in an example you have already seen:
reg f;
always @ (sel or a or b)
begin : if_else
if (sel == 1)
f = a;
else
f = b;
end
becomes...
reg f;
always @ (sel or a or b)
begin : pure_if
f = b;
if (sel == 1)
f = a;
end
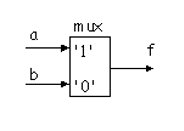
Note that the behaviour being described is the same. In the pure_if always block, f initially gets b. Only if sel is active HIGH does f get a. This is perhaps a slightly odd way to describe a multiplexing circuit but it is accepted by all synthesis tools. Synthesis tools expect to create circuits responding to binary values. As far as a synthesis tool is concerned if sel is 1 a is routed through to f. If sel is not 1 it must be 0 and thus sel being 0 leaves f being driven by the initial assignment from b.
Let's lose the b input to the always block so that we have:
reg f;
always @ (sel, a)
begin : latching_if
if (sel == 1)
f = a;
end
Incomplete Assignment
Now analyze the behaviour of the code. If sel is 1, f gets a. But what happens when sel is 0? Well, very simply, nothing! f does not and can not change. When sel is fixed at 0, we can change a as much as we like, f will not be assigned the value of a. If we suppose that an if statement synthesises to a multiplexer, then we must be able to configure the multiplexer such that f only gets the value of a when sel is 1. This can be achieved by feeding back the multiplexer f output back to the 0 input; in hardware terms this is a transparent latch and this is exactly the hardware synthesized by a synthesis tool given this Verilog code.
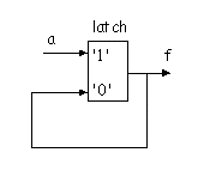
If the target architecture does not contain transparent latches the synthesis tool will generate multiplexer circuits that employ combinational feedback in order to mimic the latching behaviour required.
Now, this is very well but what's really happening here? One minute if statements create multiplexers, the next they create latches. Well, it's not the if statements, but the process as a whole that counts. If it is possible to execute an always block without assigning a value to a signal in that always block, the reg variable will be implemented as a transparent latch. This is known as incomplete assignment.
Golden Rule 2:
To synthesize combinational logic using an always block, all variables must be assigned under all conditions.
Simplifying code analysis
Suppose you are creating an always block to describe combinational logic. This always block consists of nested if-else statements as follows:
reg f, g;
always @ (sel or sel_2 or sel_3 or a or b)
begin
if (sel == 1)
begin
f = a;
if (sel_2 == 1)
g = ~ a;
else
begin
g = ~ b;
if (sel_3 == 1)
g = a ^ b;
end
end
else
begin
if (sel_2 == 1)
g = a & b;
else
if (sel_3 == 1)
g = ~(a & b);
// oops! no else
// else
// g = ...
f = b;
end
end
Will you get transparent latches on the f and g outputs? Not easy is it? If you look carefully you will see that in fact, g is latched when sel is 0, sel_2 is 0 and sel_3 is 0. The ‘oops!' comment should help you to see where the complete assignment is NOT made.
Default Assignment
Fortunately, it is possible to save yourself the bother of scouring through the always block code to locate possible incomplete assignments by setting variables to default values at the start of the always block. Using this approach you may get undesired functionality if you have missed out an assignment (which should be easy to fix) as opposed to unwanted transparent latches. For our current example,
always @ (sel or sel_2 or sel_3 or a or b)
begin
// default values assigned to f, g
f = b;
g = a & b;
if (sel == 1)
begin
f = a;
if (sel_2 == 1)
g = ~ a;
else
begin
g = ~ b;
if (sel_3 == 1)
g = a ^ b;
end
end
else
if (sel_2 == 1)
g = a & b;
else
if (sel_3 == 1)
g = ~(a & b);
end
Prev




